Técnicas de conteo (cómo ganar el Bonoloto)
Clase de Matemáticas
Hola, ¿cómo están?
Hoy comenzaré a escribir sobre un tema muy importante y que no tiene tanta difusión como las derivadas e integrales: técnicas de conteo.
Es fundamental para materias como Probabilidad y Estadística y Matemáticas Discretas, entre otras.
Como siempre si prefieres ver un video en lugar de leer, puedes ir a este enlace.
Si prefieres leer, comencemos con el tema.
¿Por qué necesitamos saber manejar técnicas de conteo?
La respuesta a la pregunta que inicia esta sección es porque hay casos que no nos sirve tratar de individualizar cada uno de los casos que necesitamos contar, sería muy factible que nos perdamos en el camino o nos demandaría demasiado tiempo.
Por ejemplo, si quisiéramos saber cuántas cadenas de dos caracteres podríamos escribir con estas tres letras: A, B y C (sin repetirlas), sería lógico que tratemos de escribirlas. De esta forma obtendríamos:
AB
AC
BA
BC
CA
CB
Contamos, y vemos que son 6 cadenas diferentes. Pero si el problema fuera con todas las letras del abecedario y las cadenas deberían tener longitud 8, ya el planteo manual no sería viable.
2. Factorial de un número
Antes de entrar de lleno en las técnicas de conteo, necesitamos saber qué es el factorial de un número. Dicho número debe ser un entero mayor o igual a 0.
El factorial de un número n (entero positivo) se calcula como el producto de todos los enteros positivos menores o iguales a n, y la notación se indica con un signo de admiración de cierre detrás del número.
Ejemplo:
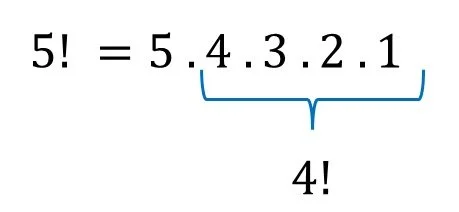
Pero teniendo en cuenta que
el factorial de 5, es lo mismo que multiplicar 5, por el factorial de 4, podríamos definir la función factorial de manera recursiva.
El factorial de un valor entero positivo, es dicho valor multiplicado el factorial de su predecesor.
Esta definición la vamos a utilizar bastante a la hora de hacer ciertas simplificaciones y ahorrarnos muchas cuentas.
Por ejemplo, si quisiéramos calcular el factorial de 40, partido el factorial de 38, deberíamos hacer muchos cálculos si no utilizáramos la definición recursiva.
Simplificación de factoriales utilizando la definición recursiva
Importante: 0! = 1
El factorial de 0, es un caso particular: existe, y vale 1. Esto lo necesitamos para poder aplicar la definición recursiva: si
Despejando (n - 1)! queda:
Al reemplazar n por el valor 1, nos queda que 1 / 1 = 0! Por lo tanto: 0! = 1
3. Combinando elementos de varios conjuntos
Ahora sí, comencemos con el tema que nos ocupa.
Supongamos que necesitamos vestirnos y contamos solamente con un pantalón negro y una camisa blanca.
Lo que va a suceder es que solamente podamos vestirnos de una sola manera: combinando el pantalón negro con la camisa blanca.
Pero, si a nuestro vestuario le agregáramos un pantalón gris y dos camisas: una celeste y otra amarilla, podríamos vestirnos de 6 maneras diferentes.
Si elegimos el pantalón negro, lo podemos combinar con cualquiera de las tres camisas: la blanca, la celeste y la amarilla. Lo mismo sucede con el pantalón gris.
Es decir, la cantidad de combinaciones será la cantidad de elementos de un conjunto (el de pantalones) multiplicada la cantidad de elementos del otro conjunto (camisas). En este caso es
2 x 3 = 6
Importante: el orden en la elección no nos interesa. Quedaremos vestidos de la misma forma si elegimos primero el pantalón negro y luego la camisa celeste, que si lo hacemos al revés.
Si agregáramos un nuevo conjunto: pares de zapatos. Formado por un par negro y otro marrón, tendríamos las 6 combinaciones de pantalones y camisas, relacionadas con cada uno de los pares de zapatos. Es decir:
2 x 3 x 2 = 12 formas distintas de vestirnos.
4. Combinando elementos de un mismo conjunto
Supongamos que ganamos un concurso de tiro al blanco en una feria y nos dan a elegir dos premios de una serie de juguetes que tienen en exhibición.
Podemos elegir dos premios entre un balón, una muñeca, un unicornio inflable, una diadema, un osito de peluche, una baraja de naipes y un autobús.
Aclaración importante: no podríamos elegir dos veces el mismo premio, por ejemplo, dos balones.
Una elección sería, por ejemplo, el balón y el osito. Otra, la diadema y la muñeca.
¿Cuántas elecciones o combinaciones diferentes podemos realizar?
Nuevamente, es importante decidir si el orden en la elección cambia en algo al resultado. La respuesta es: no. Es lo mismo pedir en primer lugar el balón y luego el osito, que hacerlo al revés. Nos quedaremos con los dos premios de ambas maneras.
Cuando sucede esto, decimos que es un problema de combinatoria, sin repetición (no podemos elegir más de una vez el mismo premio).
Nota: el problema anterior también era un problema combinatorio, pero combinando elementos de conjuntos diferentes: pantalones, camisas y zapatos. Aquí, el conjunto de donde elegimos es único.
La notación y la fórmula es la siguiente:
Donde n es la cantidad total de elementos, en este ejemplo, 7, y k es la cantidad de elementos que debemos elegir. En este caso, k = 2.
Resultado:
Tenemos 21 combinaciones diferentes de elegir los juguetes. Un buen ejercicio sería que apuntaras todas las combinaciones para comprobarlo. El consejo es comenzar con el primer juguete y combinarlo con todos los demás, luego, continuar con el segundo, etc.
Ejemplo: balón y muñeca, balón y unicornio, balón y diadema, balón y osito, balón y naipes, balón y autobús. Ahora, pasamos a elegir primero la muñeca, pero ¡cuidado! Muñeca y balón, no hay que seleccionarla, porque esa combinación ya fue elegida y la estaríamos contando dos veces. Comenzaríamos con muñeca y unicornio, etc.
5. Cómo ganar el Bonoloto
El Bonoloto es un juego que consiste en elegir 6 números entre el 1 y el 49, luego se sortean los números y quien acierta los 6 dígitos, gana el juego.
Hay otros premios menores pero aquí nos vamos a centrar en el premio mayor.
¿Cómo hacer para ganar el juego? Es muy sencillo: debemos apostar a todas las posibles combinaciones, de esa forma nos aseguramos ganar el premio mayor.
Entonces, la pregunta es ¿cuántas combinaciones hay?
Tarea: piensa en 30 segundos si es un problema combinatorio y apúntalo. Luego, continúa leyendo.
Si apuntaste que es un problema combinatorio, que el orden no interesa ¡felicitaciones! Estás en lo correcto. De lo contrario, no te desanimes, estos ejercicios se empiezan a entender con la práctica.
El orden no nos interesa, si, por ejemplo, uno de los números que elijo es el 15 (mi número favorito), será indistinto que en el sorteo salga el 15 en primer lugar o en el quinto lugar. Tendré una coincidencia de todas maneras.
Por lo tanto, la fórmula de combinatoria que debemos usar es n = 49 y k = 6.
Redondeando, deberíamos hacer unas 14 millones de apuestas. A 50 céntimos cada una, tendremos que invertir unos 7 millones de euros. Seguramente, el premio mayor sea menor que esa cifra, por lo que perderíamos dinero, pero quién nos quitaría la felicidad de decir ¡he ganado el Bonoloto!
Resumen
El factorial de un número es un valor que se obtiene multiplicando todos los enteros positivos menores o iguales a dicho número.
El factorial de 0 existe y vale 1.
En los problemas combinatorios, el orden de la elección no cuenta.
Podemos tener problemas combinatorios entre diferentes conjuntos: la cantidad de combinaciones será el producto de la cardinalidad (cantidad de elementos) de cada uno de los conjuntos.
Podemos tener problemas combinatorios eligiendo elementos de un solo conjunto (sin repeticiones). En este caso, la cantidad de combinaciones surge de la siguiente fórmula:
Puedes enviar tus comentarios o consultas, te contestaré a la brevedad.